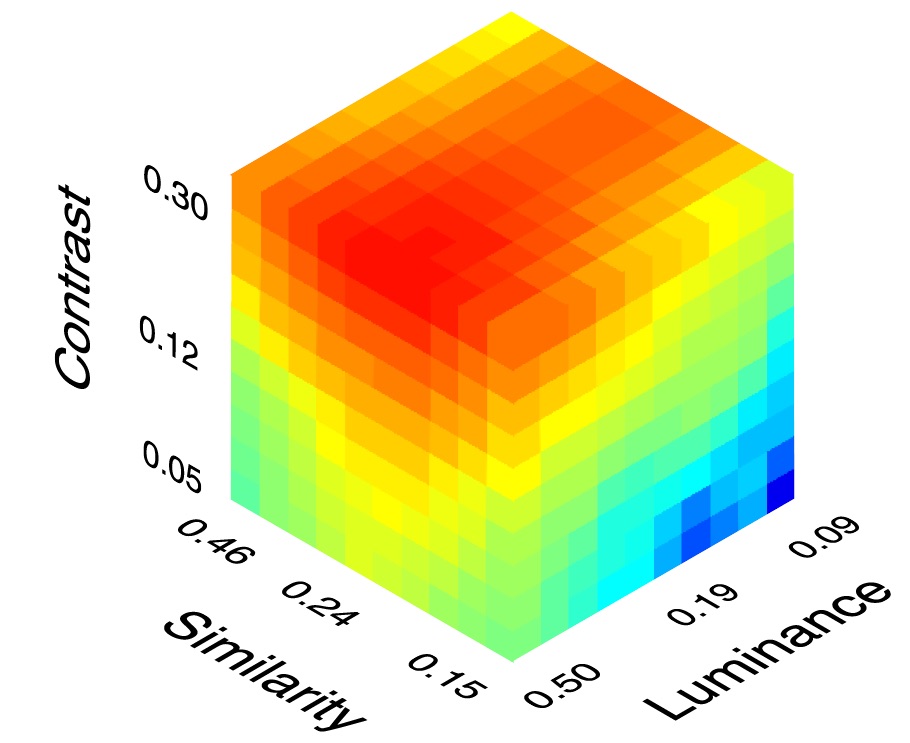
A fundamental everyday visual task is to identify specific target objects within a background scene.  Under natural conditions, both the properties of the background and the amplitude of the target (if present) are generally different on every occasion. To gain some understanding of identification under such natural conditions we determined the amplitude thresholds in natural images of a matched-template observer, as a function of the three local background properties: luminance, contrast, and phase-invariant similarity to the target. We found that threshold (which is equal to the standard deviation of the template response) is a linear separable function (the product) of all three dimensions—“multidimensional Weber’s law.”  This fact poses a serious problem for detecting targets under natural conditions, where both the properties of the background and the target amplitude are uncertain. Specifically, good performance requires a different decision criterion on the template responses for each possible combination of background properties. However, we show that divisively normalizing the template (feature) responses by the product of the locally estimated luminance, contrast, and similarity creates a distribution of template responses that is normal with a standard deviation of 1.0, independent of the background properties. Thus, for any desired false-alarm rate the optimal hit rate can be obtained with a single decision criterion, even under maximum uncertainty. This is just the sort of normalization (gain-control) observed early in the visual system for the dimensions of luminance and contrast, and perhaps for similarity. In psychophysical experiments, we show that human performance is consistent with this normalized matched template observer (which has only a single efficiency parameter). We argue that the rapid and local neural gain-control mechanisms, and the psychophysical laws of masking, are most likely the result of evolving a near optimal solution to identification in natural backgrounds under conditions of high uncertainty.